Current Research Projects

• Phase Transitions and Transport Phenomena in Monolayer and Bilayer Graphene
• Topological Quantum Computing Via Topological Insultors
• Conductivity of Strongly Interacting Systems

Phase Transitions and Transport Phenomena in Monolayer and Bilayer Graphene

We seek to study the collective motion of charge quasi-particles in bilayer heterojunctions consisting of monolayers of graphene separated by a tunnel dielectric as a means of generating low-power logic switches with significant drive currents.. In a switch that is based on a set of independently-moving electrons, switching requires a change in gate voltage large enough to shift each electron’s energy by more than the room temperature thermal energy. With the collective motion of electrons, one may hope to achieve switching with smaller changes in gate voltage: the energy of an entire ensemble of electrons can be shifted by more than room temperature thermal energy, turning on transport, even though each electron’s energy is shifted by only a small fraction of that amount. Normally collective effects only exist under extreme conditions, however, the unique properties of graphene may allow these effects to persist at room temperature. I propose to study these devices theoretically using a combination of non-equilibrium Green's functions and novel quantum Monte Carlo techniques with the stated goal of understanding: the stability of the collective effects under a variety of conditions, the non-equilibrium switching response, and the importance of materials properties and quality.

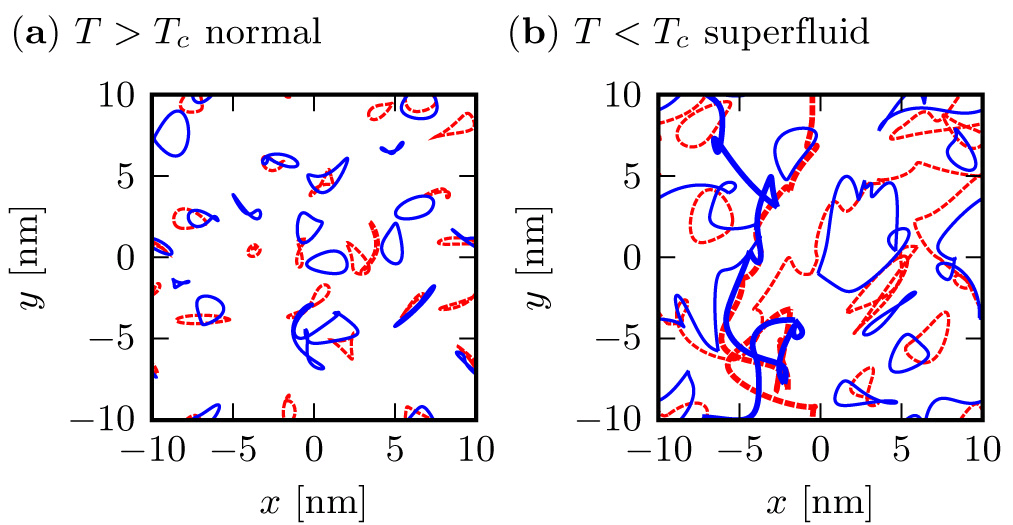
The figure to the right shows the typical paths for electrons and holes in a quasi-particle path integral Monte Carlo simulation of bilayer graphene with a separation between the layers of 0.5 nm. In the figure, the red dashed lines represent the hole quasi-particles and the blue solid lines represent the electron quasi-particles. The purpose of this simulation is to show the transition from a normal Fermi liquid to an excitonic superfluid. In (a), we are above the transition temperature and the excitons are localized by the thermal wavelength and do not connect around the periodic simulation cell. In (b), we are now below the transition temperature and the excitons condense forming a superfluid. This manifests itself as long permuting paths which wind around the simulation domain.

Topological Quantum Computing Via Topological Insultors

Spin has long been known to have the potential to perform universal quantum computation. To realize quantum computation with spins one needs an extraordinary amount of control over the spins so we can set, manipulate, and read out the various processes required in information processing. This is a daunting task as these processes are not immune from decoherence. While one can manipulate single spins with high-fidelity and long coherence times, there is no clear path to move from single spin manipulation to many spins. Recent advances have revealed a new type of information processing, topological quantum computation, which is immune from environment related decoherence. Topological information processing relies on the manipulation of anyons, particles which obey non-Abelian statistics. The simplest of these particles, Majorana fermions, are believed to exist as excitations in exotic materials under extreme conditions. Additionally, Majorana fermions have been proposed to exist in a new class of materials commonly referred to as topological insulators coupled with superconducting contacts under much less extreme conditions. In this work, we propose to theoretically investigate the formation, manipulation, entanglement and detection of Majorana fermions in hybrid topological insulator structures. Furthermore, we seek to further investigate the relationship between superconducting elements and 2D and 3D topological insulators. The tasks we outline in this proposal will be undertaken using a variety of analytical tools to provide insight into the system behavior at the theoretical limits and numerical techniques to yield results in experimentally realistic conditions. The goal is to make significant and measurable advances towards transformative information processing technologies which have the potential to vastly increase operational capabilities of multiple applications.

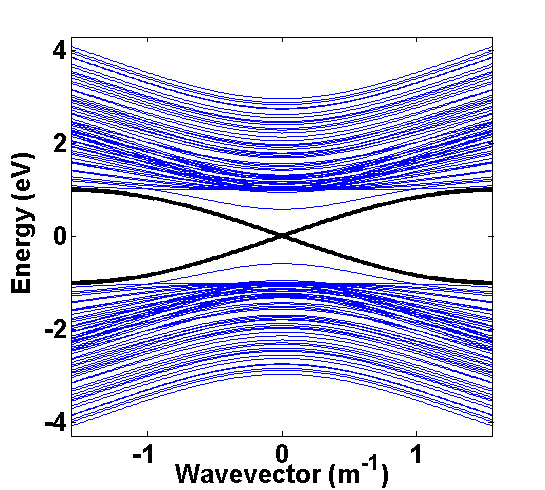
In this figure, we calculate the dispersion relationship for a generic topological insulator. Here we can clearly see the topologically protected chiral Dirac excitation at zero energy. Understanding of these states could lead to very interesting new physical phenomena.

Conductivity of Strongly Interacting Systems

The inexorable shrinking of nanosystems has resulted in the discovery of a plethora of intersting phenomena. Heretofore, many nanoscale structures of interest could be adequately described by traditional single electron methods such as non-equilibrium Green’s functions (NEGF). Nevertheless, as the lithographic and semiconductor growth techniques have improved, so too has our ability to explore the one-dimensional (1D) limit of nanostructures. The transport of electrons in these systems can exhibit strong many body effects. These are often understood in terms of from the Landauer-Buttiker formula for a two-point conductance measurement. While this equation is often used in an effective single-particle framework, such as Kohn-Sham density functional theory (KS-DFT), the formalism also applies to many-body theories. Of the many relevent examples of the deviation from single particle theory present in the literature, some of the most striking are the so-called ‘0.7’ plateau in the conductance of a quantum junction, the observation of Luttinger liquid behavior in narrow quantum wires, and carbon nanotubes. As an alternative, we seek to apply quantum Monte Carlo (QMC) techniques, which have proven very useful in establishing robust numerical results for physical systems, to the problem of calculating the conductivity of stongly interacting systems. We have been working to apply path integral quantum Monte Carlo techniques to the calculation electrical conductivity of strongly interacting systems through the use of the Kubo formula.

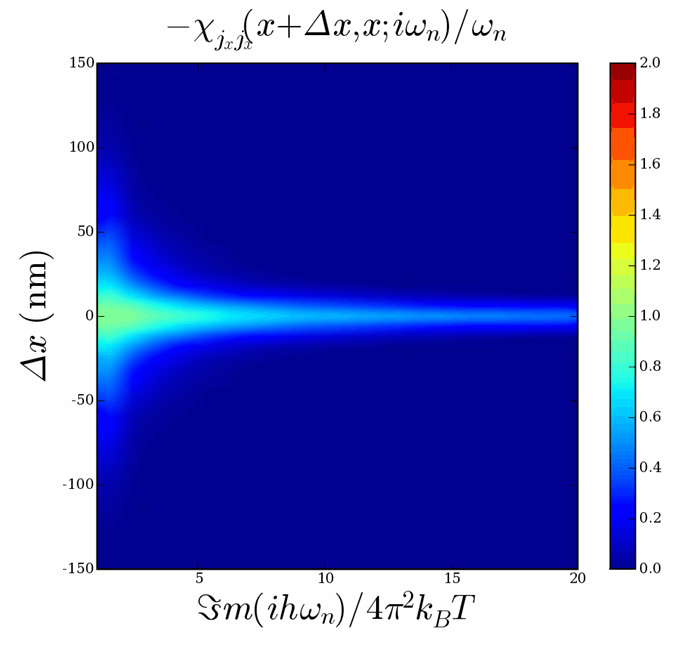
In the figure to the right, we plot the current-current response function as a function of position and imaginary frequency for a 500 nm long quantum wire containing 30 spin up electrons. We take the DC limit to get the conductivity.

Previous Research Projects

• Transport and Decoherence in Nanowire MOS Transistors
• Coupled Quantum Waveguide System
• Spin Filtering in Quantum Systems